Reduction¶

A key advantage of this package are highly optimized reduction and map-reduction functions, which sometimes lead to over 10x speed up.

Basic reduction functions¶

The package extends/specializes sum, mean, max, and min, not only providing substantially better performance, but also allowing reduction over function results. It also provides sum!, mean!, max!, and min!, which allow writing results to pre-allocated storage when performing reduction along specific dimensions.

The function sum and its variant forms:

sum(x)
sum(f1, x)            # compute sum of f1(x)
sum(f2, x1, x2)       # compute sum of f2(x1, x2)
sum(f3, x1, x2, x3)   # compute sum of f3(x1, x2, x3)

sum(x, dim)
sum(f1, x, dim)
sum(f2, x1, x2, dim)
sum(f3, x1, x2, x3, dim)

sum!(dst, x, dim)    # write results to dst
sum!(dst, f1, x1, dim)
sum!(dst, f2, x1, x2, dim)
sum!(dst, f3, x1, x2, x3, dim)

sumfdiff(f2, x, y)     # compute sum of f2(x - y)
sumfdiff(f2, x, y, dim)
sumfdiff!(dst, f2, x, y, dim)

The function mean and its variant forms:

mean(x)
mean(f1, x)            # compute mean of f1(x)
mean(f2, x1, x2)       # compute mean of f2(x1, x2)
mean(f3, x1, x2, x3)   # compute mean of f3(x1, x2, x3)

mean(x, dim)
mean(f1, x, dim)
mean(f2, x1, x2, dim)
mean(f3, x1, x2, x3, dim)

mean!(dst, x, dim)    # write results to dst
mean!(dst, f1, x1, dim)
mean!(dst, f2, x1, x2, dim)
mean!(dst, f3, x1, x2, x3, dim)

meanfdiff(f2, x, y)     # compute mean of f2(x - y)
meanfdiff(f2, x, y, dim)
meanfdiff!(dst, f2, x, y, dim)

The function max and its variants:

max(x)
max(f1, x)            # compute maximum of f1(x)
max(f2, x1, x2)       # compute maximum of f2(x1, x2)
max(f3, x1, x2, x3)   # compute maximum of f3(x1, x2, x3)

max(x, (), dim)
max(f1, x, dim)
max(f2, x1, x2, dim)
max(f3, x1, x2, x3, dim)

max!(dst, x, dim)    # write results to dst
max!(dst, f1, x1, dim)
max!(dst, f2, x1, x2, dim)
max!(dst, f3, x1, x2, x3, dim)

maxfdiff(f2, x, y)     # compute maximum of f2(x - y)
maxfdiff(f2, x, y, dim)
maxfdiff!(dst, f2, x, y, dim)

The function min and its variants

min(x)
min(f1, x)            # compute minimum of f1(x)
min(f2, x1, x2)       # compute minimum of f2(x1, x2)
min(f3, x1, x2, x3)   # compute minimum of f3(x1, x2, x3)

min(x, (), dim)
min(f1, x, dim)
min(f2, x1, x2, dim)
min(f3, x1, x2, x3, dim)

min!(dst, x, dim)      # write results to dst
min!(dst, f1, x1, dim)
min!(dst, f2, x1, x2, dim)
min!(dst, f3, x1, x2, x3, dim)

minfdiff(f2, x, y)     # compute minimum of f2(x - y)
minfdiff(f2, x, y, dim)
minfdiff!(dst, f2, x, y, dim)

Note: when computing maximum/minimum along specific dimension, we use max(x, (), dim) and min(x, (), dim) instead of max(x, dim) and min(x, dim) to avoid ambiguities that would otherwise occur.

Generic folding¶

This package extends foldl and foldr for generic folding.

# suppose length(x) == 4

foldl(op, x)     # i.e. op(op(op(x[1], x[2]), x[3]), x[4])
foldr(op, x)     # i.e. op(x[1], op(x[2], op(x[3], x[4])))

foldl(Add(), x)   # sum over x from left to right
foldr(Add(), x)   # sum over x from right to left

You can also use functors to generate terms for folding.

foldl(op, f1, x)    # fold over f1(x) from left to right
foldr(op, f1, x)    # fold over f1(x) from right to left

foldl(op, f2, x1, x2)   # fold over f2(x1, x2) from left to right
foldr(op, f2, x1, x2)   # fold over f2(x1, x2) from right to left

foldl(op, f3, x1, x2, x3)   # fold over f3(x1, x2, x3) from left to right
foldr(op, f3, x1, x2, x3)   # fold over f3(x1, x2, x3) from right to left

foldl_fdiff(op, f, x, y)   # fold over f(x - y) from left to right
foldr_fdiff(op, f, x, y)   # fold over f(x - y) from right to left

You may also provide an initial value s0 for folding.

foldl(op, s0, x)
foldr(op, s0, x)

foldl(op, s0, f1, x)
foldr(op, s0, f1, x)

foldl(op, s0, f2, x1, x2)
foldf(op, s0, f2, x1, x2)

foldl(op, s0, f3, x1, x2, x3)
foldr(op, s0, f3, x1, x2, x3)

foldl_fdiff(op, s0, f, x, y)
foldr_fdiff(op, s0, f, x, y)

The function foldl also supports reduction along a specific dim.

foldl(op, s0, x, dim)                # fold op over x along dimension dim
foldl(op, s0, f1, x, dim)            # fold op over f1(x) along dimension dim
foldl(op, s0, f2, x1, x2, dim)       # fold op over f2(x1, x2) along dimension dim
foldl(op, s0, f3, x1, x2, x3, dim)   # fold op over f3(x1, x2, x3) along dimension dim
foldl_fdiff(op, s0, f, x, y, dim)    # fold op over f(x - y) along dimension dim

# the following statement write results to pre-allocated storage

foldl!(dst, op, s0, x, dim)
foldl!(dst, op, s0, f1, x, dim)
foldl!(dst, op, s0, f2, x1, x2, dim)
foldl!(dst, op, s0, f3, x1, x2, x3, dim)
foldl_fdiff!(dst, op, s0, f, x, y, dim)

Derived reduction functions¶

In addition to these basic reduction functions, we also define a set of derived reduction functions, as follows:

var(x)
var(x, dim)
var!(dst, x, dim)

std(x)
std(x, dim)
std!(dst, x, dim)

sumabs(x)  # == sum(abs(x))
sumabs(x, dim)
sumabs!(dst, x, dim)

meanabs(x)   # == mean(abs(x))
meanabs(x, dim)
meanabs!(dst, x, dim)

maxabs(x)   # == max(abs(x))
maxabs(x, dim)
maxabs!(dst, x, dim)

minabs(x)   # == min(abs(x))
minabs(x, dim)
minabs!(dst, x, dim)

sumsq(x)  # == sum(abs2(x))
sumsq(x, dim)
sumsq!(dst, x, dim)

meansq(x)  # == mean(abs2(x))
meansq(x, dim)
meansq!(dst, x, dim)

dot(x, y)  # == sum(x .* y)
dot(x, y, dim)
dot!(dst, x, y, dim)

sumabsdiff(x, y)   # == sum(abs(x - y))
sumabsdiff(x, y, dim)
sumabsdiff!(dst, x, y, dim)

meanabsdiff(x, y)   # == mean(abs(x - y))
meanabsdiff(x, y, dim)
meanabsdiff!(dst, x, y, dim)

maxabsdiff(x, y)   # == max(abs(x - y))
maxabsdiff(x, y, dim)
maxabsdiff!(dst, x, y, dim)

minabsdiff(x, y)   # == min(abs(x - y))
minabsdiff(x, y, dim)
minabsdiff!(dst, x, y, dim)

sumsqdiff(x, y)  # == sum(abs2(x - y))
sumsqdiff(x, y, dim)
sumsqdiff!(dst, x, y, dim)

meansqdiff(x, y)  # == mean(abs2(x - y))
meansqdiff(x, y, dim)
meansqdiff!(dst, x, y, dim)

Although this is quite a large set of functions, the actual code is quite concise, as most of such functions are generated through macros (see src/reduce.jl)

In addition to the common reduction functions, this package also provides a set of statistics functions that are particularly useful in probabilistic or information theoretical computation, as follows

sumxlogx(x)  # == sum(xlogx(x)) with xlog(x) = x > 0 ? x * log(x) : 0
sumxlogx(x, dim)
sumxlogx!(dst, x, dim)

sumxlogy(x, y)  # == sum(xlog(x,y)) with xlogy(x,y) = x > 0 ? x * log(y) : 0
sumxlogy(x, y, dim)
sumxlogy!(dst, x, y, dim)

entropy(x)   # == - sumxlogx(x)
entropy(x, dim)
entropy!(dst, x, dim)

logsumexp(x)   # == log(sum(exp(x)))
logsumexp(x, dim)
logsumexp!(dst, x, dim)

softmax!(dst, x)    # dst[i] = exp(x[i]) / sum(exp(x))
softmax(x)
softmax!(dst, x, dim)
softmax(x, dim)

For logsumexp and softmax, special care is taken to ensure numerical stability for large x values, that is, their values will be properly shifted during computation (e.g. you can perfectly do logsumexp([1000., 2000., 3000.])) with this package, while log(sum(exp([1000., 2000., 3000.]))) would lead to overflow.)

Weighted Sum¶

Computation of weighted sum as below is common in practice.

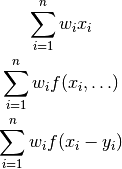
$\sum_{i=1}^n w_i x_i \sum_{i=1}^n w_i f(x_i, \ldots) \sum_{i=1}^n w_i f(x_i - y_i)$

NumericExtensions.jl directly supports such computation via wsum and wsumfdiff:

wsum(w, x)                 # weighted sum of x with weights w
wsum(w, f1, x1)            # weighted sum of f1(x1) with weights w
wsum(w, f2, x1, x2)        # weighted sum of f2(x1, x2) with weights w
wsum(w, f3, x1, x2, x3)    # weighted sum of f3(x1, x2, x3) with weights w
wsumfdiff(w, f2, x, y)    # weighted sum of f2(x - y) with weights w

These functions also support computing the weighted sums along a specific dimension:

wsum(w, x, dim)
wsum!(dst, w, x, dim)

wsum(w, f1, x1, dim)
wsum!(dst, w, f1, x1, dim)

wsum(w, f2, x1, x2, dim)
wsum!(dst, w, f2, x1, x2, dim)

wsum(w, f3, x1, x2, x3, dim)
wsum!(dst, w, f3, x1, x2, x3, dim)

wsumfdiff(w, f2, x, y, dim)
wsumfdiff!(dst, w, f2, x, y, dim)

Furthermore, wsumabs, wsumabsdiff, wsumsq, wsumsqdiff are provided to compute weighted sum of absolute values / squares to simplify common use:

wsumabs(w, x)              # weighted sum of abs(x)
wsumabs(w, x, dim)
wsumabs!(dst, w, x, dim)

wsumabsdiff(w, x, y)       # weighted sum of abs(x - y)
wsumabsdiff(w, x, y, dim)
wsumabsdiff!(dst, w, x, y, dim)

wsumsq(w, x)             # weighted sum of abs2(x)
wsumsq(w, x, dim)
wsumsq!(dst, w, x, dim)

wsumsqdiff(w, x, y)      # weighted sum of abs2(x - y)
wsumsqdiff(w, x, y, dim)
wsumsqdiff!(dst, w, x, y, dim)

Performance¶

The reduction and map-reduction functions are carefully optimized. In particular, several tricks lead to performance improvement:

computation is performed in a cache-friendly manner;
computation completes in a single pass without creating intermediate arrays;
kernels are inlined via the use of typed functors;
inner loops use linear indexing (with pre-computed offset);
opportunities of using BLAS are exploited.

Generally, many of the reduction functions in this package can achieve 3x - 12x speed up as compared to the typical Julia expression.

We observe further speed up for certain functions:

full reduction with sumabs, sumsq, and dot utilize BLAS level 1 routines, and they achieve 10x to 30x speed up.
For var and std, we devise dedicated procedures, where computational steps are very carefully scheduled such that most computation is conducted in a single pass. This results in about 25x speedup.